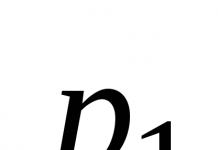Варламов А.А. Конус трения //Квант. - 1986. - № 1. - С. 24-25.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Если рассмотреть условия равновесия тела на наклонной плоскости, угол наклона которой можно изменять, то легко получить (сделайте это самостоятельно), что тело начнет соскальзывать с плоскости при угле φ таком, что

\(~\operatorname{tg} \varphi = \mu\) ,

где μ - коэффициент трения тела о плоскость. Не кажется ли вам удивительным, что этот угол не зависит от массы тела?

То же самое выражение для угла φ можно получить и другим, пожалуй, более простым способом. Но для этого надо предварительно познакомиться с понятием «конус трения».

Пусть тело, которое можно считать материальной точкой, находится на шероховатой горизонтальной плоскости. Сила тяжести \(~m \vec g\) прижимает тело к поверхности, и поверхность «откликается», действуя на тело силой нормального давления \(~\vec N\). Если же к телу приложена также и некоторая горизонтальная сила, то со стороны поверхности появляется еще одна сила - сила трения. Пока величина горизонтальной силы не превышает максимального значения силы трения покоя F тр.п. max = μN , тело покоится. При достижении этого значения тело начинает двигаться, причем поверхность действует на него препятствующей движению силой трения скольжения

\(~F_{tr.sk.} = F_{tr.p.max} = \mu N\) .

Как сила нормальной реакции, так и сила трения порождаются поверхностью, поэтому можно говорить о полной силе реакции поверхности. В случае, когда тело под действием внешней силы (конечно, включающей в себя силу тяжести) движется вдоль поверхности (рис. 1), полная сила реакции есть

\(~\vec R = \vec N + \vec F_{tr.sk}\) .

Эта сила направлена под углом φ к нормали, который легко определить:

\(~\operatorname{tg} \varphi = \frac{F_{tr.sk}}{N} = \mu ; \varphi = \operatorname{arctg} \mu\) .

Угол φ называют углом трения.

Будем теперь мысленно вращать вектор \(~\vec R\) вокруг нормали к поверхности, не меняя угла φ между ними. При этом вектор опишет конус (с углом 2φ при вершине), называемый конусом трения . Он обладает следующим замечательным свойством. Какая бы большая по величине внешняя сила не прикладывалась к телу, если она лежит внутри конуса трения, тело остается в покое. Если же эта сила выходит за пределы конуса трения, то, какой бы малой она не была, тело начинает двигаться.

В справедливости этого утверждения убедиться нетрудно. Действительно, пусть внешняя сила \(~\vec F\) (см. рис. 1) приложена к телу так, что ее линия действия составляет угол α с нормалью к поверхности. Тогда «сдвигающая» тело вдоль поверхности сила равна F sin α , а сила нормальной реакции равна F cos α . Таким образом, предельно возможная сила трения покоя, удерживающая тело на месте, есть

\(~F_{tr.p.max} = \mu N = \mu F \cos \alpha = F \operatorname{tg} \varphi \cos \alpha\) .

Пока сила \(~\vec F\) лежит внутри конуса трения, α < φ и, следовательно, F sin α < F tg φ cos α . Тело при этом покоится. Однако как только угол α становится больше угла трения φ , последнее неравенство нарушается. Теперь трение уже не в состоянии удержать тело на месте, и оно начинает скользить. Вернемся к телу, оставленному в начале статьи на наклонной плоскости, и построим для него конус трения (рис. 2).

Внешней силой здесь служит сила тяжести \(~m \vec g\) направленная вертикально вниз. Пока α < φ , согласно сказанному выше, тело будет покоиться. Но как только угол α превысит угол φ - начнется движение. Поэтому мы сразу же получаем условие начала соскальзывания тела с наклонной плоскости:

\(~\operatorname{tg} \alpha > \mu ; \alpha > \operatorname{arctg} \mu\) .

Заметим, что понятием конуса трения пользуются инженеры при расчете той или иной конструкции. Так, например, даже при проектировании табуретки следует помнить о конусе трения.

Представьте себе табуретку, ножки которой соединены с сидением шарнирами (рис. 3). Конечно, в действительности никто не станет так делать, однако такая система крепления позволит нам легче разобраться с ролью конуса трения. Поставим такую табуретку на пол так, чтобы угол α , который ножки составляют с нормалью к полу, был меньше угла трения φ . В этом случае как бы мы не нагружали табуретку, ножки ее не разъедутся - сила, с которой каждая ножка действует на пол, лежит в пределах соответствующего конуса трения. Если же угол α сделать больше угла φ , то сила, с которой ножка действует на пол, выйдет за пределы конуса трения, ножки разъедутся и табуретка упадет.

У реальной табуретки ножки соединены с сидением не с помощью шарниров, а вклеены или вкручены в него.

Однако если сделать так, чтобы угол α превысил угол трения φ , то в месте соединения ножек табуретки с сидением могут возникнуть значительные напряжения и табуретка сломается.

Многие задачи на равновесие тела на шероховатой поверхности, т.е. при наличии трения, удобно решать геометрически. Для этого введем понятие угла и конуса трения.

Реакция реальной (шероховатой) связи слагается из двух составляющих: нормальной реакции и перпендикулярной ей силы трения . Следовательно, реакция связи отклоняется от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до максимальной, сила реакции меняется от нуля до , а ее угол с нормалью растет от нуля до некоторого предельного значения  .

Углом трения называется наибольший угол между предельной силой реакции шероховатой связи и нормальной реакцией .

Угол трения зависит от коэффициента трения.

Конусом трения называют конус, описанный предельной силой реакции шероховатой связи вокруг направления нормальной реакции.

Пример.

Если к телу, лежащему на шероховатой поверхности, приложить силу Р, образующую угол с нормалью, то тело сдвинется только тогда, когда сдвигающее усилие  будет больше предельной силы трения  (если пренебречь весом тела, то но неравенство

Выполняется только при , т.е. при ,

Следовательно, ни какой силой, образующей с нормалью угол , меньший угла трения  тело вдоль данной поверхности сдвинуть нельзя.

Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.

Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

Пример.

Рассмотрим тело имеющее вертикальную плоскость симметрии. Сечение тела этой плоскости имеет форму прямоугольника. Ширина тела равна 2a.

К телу в точке С, лежащей на оси симметрии, приложена вертикальная сила и в точке А, лежащей на расстоянии h от основания, горизонтальная сила . Реакция плоскости основания (реакция связи) приводится к нормальной реакции и силе трения . Линия действия силы неизвестна. Расстояние от точки С до линии действия силы обозначим x. (). Составим три уравнения равновесия:

Согласно закону Кулона , т.е. . (1)

Так как , то (2)

Проанализируем полученные результаты:

Будем увеличивать силу .

1) Если , то равновесие будет иметь место до тех пор, пока сила трения не достигнет своей предельной величины, условие (1) превратится в равенство. Дальнейшее увеличение силы приведет к скольжению тела по поверхности.

2) Если , то равновесие будет иметь место до тех пор, пока сила трения не достигнет величины , условие (2) превратится в равенство. Величина x будет равна h. Дальнейшее увеличение силы приведет к тому, что тело станет опрокидываться вокруг точки B (скольжения не будет).

Трение качения

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Рассмотрим цилиндрический каток радиуса r на горизонтальной плоскости. Под катка и плоскости в месте их соприкосновения могут возникнуть реакции, препятствующие действием активных сил каток может катиться по плоскости. Из-за деформации поверхностей не только скольжению, но и качению.

Активные силы, действующие на катки в виде колес, обычно состоят из силы тяжести , горизонтальной силы , приложенной к центру катка, и пары сил с моментом , стремящейся катить колесо. Колесо в этом случае называется ведомо-ведущим . Если , а , то колесо называется ведомым. Если , а , то колесо называется ведущим .

Соприкосновение катка с неподвижной плоскостью из-за деформации катка и плоскости происходит не в точке, а по некоторой линии BD. По этой линии на каток действуют распределенные силы реакции. Если привести силы реакции к точке А, то в этой точке получим главный вектор этих распределенных сил с составляющими (нормальная реакция) и (сила трения скольжения), а также пару сил с моментом .

Рассмотрим равновение катка. Система сил – плоская. Запишем уравнения равновесия системы сил.

Момент называется моментом трения качения. Наибольшее значение М достигается в момент начала качения катка по плоскости.

Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующих качению.

1. Наибольший момент пары сил, препятствующих качению, в довольно широких пределах не зависит от радиуса катка.

2. Предельное значение момента пропорционально нормальной реакции .

Коэффициент пропорциональности k называют коэффициентом трения качения при покое. Размерность k - это размерность длины.

3. Коэффициент трения качения k зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.

Тогда закон движения системы запишется в виде:

где F ik - внутренние силы взаимодействия i-й и k-й частиц
системы между собой;
F i - равнодействующая внешних сил, приложенных к i-й частице.

Согласно третьему закону Ньютона каждая пара частиц действует друг на друга с силами, равными по величине и противоположными по направлению F ik = -F ki . Следовательно, результирующая внутренних сил равняется нулю и

скорость изменения импульса системы P равняется векторной сумме внешних сил F i , действующих на частицы этой системы.

. (5)

Уравнение (5) справедливо для любого момента времени и не зависит от конкретного способа взаимодействия частиц между собой. Изменение импульса системы за конечный промежуток времени можно рассчитать, произведя суммирование импульсов внешних сил по отдельным участкам движения в соответствии с уравнением (8).

. (8)

Изменение импульса системы за конечный промежуток времени t равно определенному интегралу от импульса равнодействующей внешних сил.

Лекция 3. Расчет ферм. Трение скольжения и качения.

В данной лекции рассматриваются следующие вопросы

1. Расчет ферм.

2. Понятие о ферме.

3. Аналитический расчет плоских ферм.

4. Графический расчет плоских ферм.

5. Трение.

6. Законы трения скольжения.

7. Реакции шероховатых связей.

8. Угол трения.

9. Равновесие при наличии трения.

10. Трение качения и верчения.

11. Момент силы относительно центра как вектор.

12. Момент пары сил как вектор.

13. Момент силы относительно оси.

14. Зависимость между моментами силы относительно центра и относительно оси.

15. Приведение пространственной системы сил к данному центру.

16. Условия равновесия произвольной пространственной системы сил.

17. Задачи на равновесие тела под действием пространственной системы сил.

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

Расчет ферм. Понятие о ферме. Аналитический расчет плоских ферм.

Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложен­ные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Огра­ничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней k и число узлов n связаны соотношением

Расчет фермы сводится к определению опорных реакций и уси­лий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определе­нию усилий в стержнях.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к по­следовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

Рис.23

Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действую­щие на ферму силы парал­лельны оси х и равны: F 1 = F 2 = F 3 = F = 2.

В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соот­ношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения рав­новесия для фермы в целом, найдем, что реакции опор направлены, как пока­зано на рисунке, и численно равны;

Переходим к определению усилий в стержнях.

Пронумеруем узлы фермы римскими цифрами, а стержни - арабскими. Искомые усилия будем обозначать S 1 (в стержне 1), S 2 (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от осталь­ной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S 1 , S 2 , ... Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растя­нутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S 1 , вдоль стержня 2 - равны S 2 и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последо­вательно уравнения равновесия

Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим

F 1 +S 2 cos45 0 =0, N+S 1 +S 2 sin45 0 =0.

Отсюда находим

Теперь, зная S 1 , переходим к узлу II. Для него уравнения равнове­сия дают

S 3 +F 2 =0, S 4 -S 1 =0,

S 3 =-F=-2H, S 4 =S 1 =-1H.

Определив S 4 , составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

Наконец, для вычисления S 9 составляем уравнение равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим Y A +S 9 cos45 0 =0 откуда

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, Х А, и Y А.

Окончательные результаты расчета можно свести в таблицу:

Как показывают знаки усилий, стержень 5 растянут, остальные стер­жни сжаты; стержень 7 не нагружен (нулевой, стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обна­руживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизве­стных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера). Этим методом удобно поль­зоваться для определения усилий в отдельных стержнях фермы, в ча­стности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни рас­тянутыми (как и в методе вырезания узлов). Затем составляют урав­нения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Графический расчет плоских ферм.

Расчет фермы мето­дом вырезания узлов может производиться графически. Для этого сначала, определяют опорные реакции. Затем, последовательно отсекая от фермы каждый из ее узлов, нахо­дят усилия в стержнях, сходящихся в этих узлах, строя соответствую­щие замкнутые силовые многоугольники. Все построения проводятся в масштабе, который должен быть заранее выбран. Рас­чет начинают с узла, в котором сходятся два стержня (иначе не удастся определить неизвест­ные усилия).

Рис.24

В качестве примера рас­смотрим ферму, изображен­ную на рис. 24, а. В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лиш­них стержней. Опорные реак­ции и для рассматри­ваемой фермы, изображаем на­ряду с силами и , как известные.

Определение усилий в стержнях начинаем с рас­смотрения стержней, сходя­щихся в узле I (узлы нуме­руем римскими цифрами, а стержни - арабскими). Мысленно отрезав от этих стержней остальную часть фермы, отбрасываем ее действие отброшенной части также мысленно заменяем силами и , которые должны быть направлены вдоль стержней 1 и 2. Из сходящихся в узле I сил , и строим замкнутый треугольник (рис. 24, б). Для этого изображаем сначала в выбранном масштабе известную силу , а затем проводим через ее начало и конец прямые, параллельные стерж­ням 1 и 2. Таким путем будут найдены силы и , действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силами , , и , направленными вдоль соответствующих стержней; при этом сила нам известна, так как по равенству дей­ствия и противодействия . Построив из сил, сходящихся в узле II, замкнутый треугольник (начиная с силы ), найдем вели­чины S 3 и S 4 (в данном случае S 4 = 0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний много­угольник (для узла VI) строится для про­верки, так как все входящие в него силы уже найдены.

Из построенных многоугольников, зная масштаб, находим величины всех усилий. Знак усилия в каждом стержне опреде­ляется следующим образом. Мысленно вы­резав узел по сходящимся в нем стержням (например, узел III), прикладываем к обрезам стержней найденные силы (рис. 25); сила, направленная от узла ( на рис. 25), растягивает стержень, а си­ла, направленная к узлу ( и на рис. 25) сжимает его.

Рис.25

Соглас­но принятому условию растягивающим усилиям приписываем знак «+», а сжимающим - знак «-». В рассмотренном примере (pиc. 25) стержни 1, 2, 3, 6, 7, 9 сжаты, а стержни 5, 8 растянуты.

Трение.

Почему звучит скрипичная струна, когда по ней ведут смычком? Ведь смычок движется, а колебания струны периодические. А как разгоняется автомобиль, и какая сила замедляет его при торможении? Почему автомобиль «заносит» на скользкой дороге? Ответы на все эти и многие другие важные вопросы, связанные с движением тел, дают законы трения.

Вы видите, как разнообразно и порой неожиданно проявляется трение в окружающей нас обстановке. Трение принимает участие, и притом весьма существенное, там, где мы о нём даже и не подозреваем. Если бы трение внезапно исчезло из мира, множество обычных явлений протекало бы совершенно иным образом.

Очень красочно пишет о роли трения французский физик Гильом:

«Всем нам случалось выходить в гололедицу; сколько усилий стоило нам удерживаться от падения, сколько смешных движений приходилось нам проделать, чтобы устоять! Это заставляет нас признать, что обычно земля, по которой мы ходим, обладает драгоценным свойством, благодаря которому мы сохраняем равновесие без особых усилий. Та же мысль возникает у нас, когда мы едем на велосипеде по скользкой мостовой или когда лошадь скользит по асфальту и падает. Изучая подобные явления, мы приходим к открытию тех следствий, к которым приводит трение. Инженеры стремятся по возможности устранить его в машинах – и хорошо делают. В прикладной механике о трении говорится как о крайне нежелательном явлении, и это правильно, - однако лишь в узкой специальной области. Во всех прочих случаях мы должны быть благодарны трению: оно даёт нам возможность ходить, сидеть и работать без опасения, что книги и чернильница упадут на пол, что стол будет скользить, пока не упрётся в угол, а перо выскальзывать из пальцев.

Трение представляет настолько распространенное явление, что нам, за редкими исключениями, не приходится призывать его на помощь: оно является к нам само.

Трение способствует устойчивости. Плотники выравнивают пол так, что столы и стулья остаются там, куда их поставили. Блюдца, тарелки, стаканы, поставленные на стол, остаются неподвижными без особых забот с нашей стороны, если только дело не происходит на пароходе во время качки.

Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинки, никогда не удержатся одно на другом: всё будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкому».

К этому можно прибавить, что при отсутствии трения гвозди и винты выскальзывали бы из стен, ни одной вещи нельзя было бы удержать в руках, никакой вихрь никогда бы не прекращался, никакой звук не умолкал бы, а звучал бы бесконечным эхом, неослабно отражаясь, например, от стен комнаты.

Наглядный урок, убеждающий нас в огромной важности трения, даёт нам всякий раз гололедица. Застигнутые ею на улице, мы оказываемся беспомощными, и всё время рискуем упасть. Вот поучительная выдержка из газеты (декабрь 1927 г.):

«Лондон, 21. Вследствие сильной гололедицы уличное и трамвайное движение в Лондоне сильно затруднено. Около 1400 человек поступило в больницы с переломами рук, ног и т. д.».

«При столкновении вблизи Гайд-Парка трёх автомобилей и двух трамвайных вагонов машины были уничтожены из-за взрыва бензина…»

«Париж, 21. Гололедица в Париже и его пригородах вызвала многочисленные несчастные случаи…»

Однако, ничтожное трение на льду может быть успешно использовано технически. Уже обыкновенные сани служат тому примером. Ещё лучше свидетельствуют об этом так называемые ледяные дороги, которые устраивали для вывозки леса с места рубки к железной дороге или к пунктам сплава. На такой дороге, имеющей гладкие ледяные рельсы, две лошади тащат сани, нагруженные 70 тоннами брёвен.

Трение покоя, скольжения.

Прежде думали, что механизм трения не сложен: поверхность покрыта неровностями и трение есть результат подъёма скользящих частей на эти неровности; но это неправильно, ведь тогда не было бы потерь энергии, а на самом деле энергия на трение тратится.

Механизм потерь иной. И здесь крайне неожиданным оказывается, что эмпирически это трение можно приближенно описать простым законом. Сила нужная для того, чтобы преодолевать трение и тащить один предмет по поверхности другого, зависит от силы, направленной по нормали к поверхностям соприкосновения.

Поверхность твёрдого тела обычно обладает неровностями. Например, даже у очень хорошо отшлифованных металлов в электронный микроскоп видны «горы» и «впадины» размером в 100-1000A. При сжатии тел соприкосновение происходит только в самых высоких местах и площадь реального контакта значительно меньше общей площади соприкасающихся поверхностей. Давление в местах соприкосновения может быть очень большим, и там возникает пластическая деформация. При этом площадь контакта увеличивается, а давление падает. Так продолжается до тех пор, пока давление не достигнет определённого значения, при котором деформация прекращается. Поэтому площадь фактического контакта оказывается пропорциональной сжимающей силе.

В месте контакта действуют силы молекулярного сцепления (известно, например, что очень чистые и гладкие металлические поверхности прилипают друг к другу).

Эта модель сил сухого трения (так называют трение между твёрдыми телами), по-видимому, близка к реальной ситуации в металлах.

Если тело, например, просто лежит на горизонтальной поверхности, то сила трения на него не действует. Трение возникает, если попытаться сдвинуть тело, приложить к нему силу. Пока величина этой силы не превышает определённого значения, тело остаётся в покое и сила трения равна по величине и обратна по направлению приложенной силе. Затем начинается движение.

Может показаться удивительным, но именно сила трения покоя разгоняет автомобиль. Ведь при движении автомобиля колеса не проскальзывают относительно дороги, и между шинами и поверхностью дороги возникает сила трения покоя. Как легко видеть, она направлена в сторону движения автомобиля. Величина этой силы не может превосходить максимального значения трения покоя. Поэтому если на скользкой дороге резко нажать на газ, то автомобиль начнет буксовать. А вот если нажать на тормоза, то вращение колёс прекратится, и автомобиль будет скользить по дороге. Сила трения изменит своё направление и начнёт тормозить автомобиль.

Сила трения при скольжении твёрдых тел зависит не только от свойств поверхностей и силы давления (это зависимость качественно такая же, как для трения покоя), но и от скорости движения. Часто с увеличением скорости сила трения сначала резко падает, а затем снова начинает возрастать.

Эта важная особенность силы трения скольжения как раз и объясняет, почему звучит скрипичная струна. Вначале между смычком и струной нет проскальзывания, и струна захватывается смычком. Когда сила трения покоя достигнет максимального значения, струна сорвется, и дальше она колеблется почти как свободная, затем снова захватывается смычком и т.д.

Подобные, но уже вредные колебания могут возникнуть при обработке металла на токарном станке вследствие трения между снимаемой стружкой и резцом. И если смычок натирают канифолью, чтобы сделать зависимость силы трения от скорости более резкой, то при обработке металла приходится действовать наоборот (выбирать специальную форму резца, смазку и т.п.). Так что важно знать законы трения и уметь ими пользоваться.

Кроме сухого трения существует ещё так называемое жидкое трение, возникающее при движении твёрдых тел в жидкостях и газах и связанное с их вязкостью. Силы жидкого трения пропорциональны скорости движения и обращаются в нуль, когда тело останавливается. Поэтому в жидкости можно заставить тело двигаться, прикладывая даже очень маленькую силу. Например, тяжелую баржу на воде человек может привести в движение, отталкиваясь то дна шестом, а на земле такой груз ему, конечно, не сдвинуть. Эта важная особенность сил жидкого трения объясняет, например, тот факт, почему автомобиль «заносит» на мокрой дороге. Трение становится жидким, и даже небольшие неровности дороги, создающие боковые силы, приводят к «заносу» автомобиля.

Резюмируя вышесказанное можно заключить, что возникновение трения обусловлено, прежде всего, шероховатостью поверхностей, создающей сопротивление перемещению, и наличием сцепления у прижатых друг к другу тел. Изучение всех особенностей явления трения представляет собою довольно сложную физико-меха­ническую проблему, рассмотрение которой выходит за рамки курса теоретической механики.

В инженерных расчетах обычно исходят из ряда установленных опытным путем общих закономерностей, которые с достаточной для практики точностью отражают основные особенности явления трения. Эти закономерности, называемые законами трения скольжения при покое (законами Кулона), можно сформулировать следующим образом:

1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения(или сила сцепления), величина которой может принимать любые значения от нуля до значения F пр, называемого предельной силой трения.

Силой трения скольжения (или просто силой трения) называется составляющая силы реакции связи, которая лежит в касательной плоскости к поверхностям соприкасающихся тел.

Сила трения направлена в сторону, противоположную той, куда действующие силы стремятся сдвинуть тело.

В теоретической механике предполагается, что между поверхностями соприкасающихся тел нет смазывающего вещества.

Сухим трением называется трение, когда между поверхностями соприкасающихся тел нет смазывающего вещества.

Будем рассматривать два случая: трения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.

При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле:

Аналогично при выбранном направлении нормали нормальная реакция выражается через заданные силы:

При движении одного тела по поверхности другого сила трения является постоянной величиной.

2. Величина предельной силы трения равна произведению стати­ческого коэффициента трения на нормальное давление или нормаль­ную реакцию:

Статический коэффициент трения - число отвлеченное 0< <1; он опре­деляется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность, смазка и т. п.). Считается, что коэффициент трения не зависит от скорости движения.

3. Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой.

Объединяя вместе первый и второй законы, получаем, что при равновесии сила трения покоя (сила сцепления)

Реакции шероховатых связей. Угол трения.

До сих пор при решении задач статики мы пренебрегали трением и считали поверх­ности связей гладкими, а их реакции направленными по нормалям к этим поверхностям. Реакция реальной (шерохо­ватой) связи будет слагаться из двух составляющих: из нормальной реакции и перпендикулярной к ней силы трения . Следовательно, полная реакция будет отклонена от нормали к поверхности на не­который угол. При изменении силы трения от нуля до F пр сила R будет меняться от N до R пр, а ее угол с нормалью будет расти от нуля до некото­рого предельного значения (рис. 26).

Рис.26

Наиболь­ший угол , который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения . Из чертежа видно, что

Так как , отсюда находим следующую связь между углом трения и коэффициентом трения:

При равновесии полная реакцияR , в зависимости от сдвигающих сил, может проходить где угодно внутри угла трения. Когда равно­весие становится предельным, реакция будет отклонена от нормали на угол .

Конусом трения называют конус, описанный предельной силой реакции шероховатой связи вокруг направления нормальной реакции.

Если к телу, лежащему на шероховатой поверх­ности, приложить силуР , образующую угол с нор­малью (рис. 27), то тело сдвинется только тогда, когда сдвигающее усилие Psin будет больше (мы считаем N=Pcos , пренеб­регая весом тела). Но неравенство , в котором , выполняется только при , т.е. при . Следовательно, ни­какой силой, образующей с нормалью угол , меньший угла трения , тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или само­торможения тел.

Рис.27

Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.

Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

При стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению, называемая СИЛОЙ ТРЕНИЯ СКОЛЬЖЕНИЯ. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения (или сила сцепления), которая может принимать любые значения от нуля до значения F ПР, называемого ПРЕДЕЛЬНОЙ СИЛОЙ ТРЕНИЯ.

(F ПР = f 0 N). Равновесие, имеющее место, когда сила трения равна называется ПРЕДЕЛЬНЫМ РАВНОВЕСИЕМ.

УГОЛ ТРЕНИЯ – наибольший угол ϕ 0 , который полная реакция шероховатой связи образует с нормалью к поверхности. Из чертежа видно, что

Так как F ПР = f 0 N, то отсюда находим следующую связь между углом трения и коэффициентом трения:

При равновесии полная реакция в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол . Если к телу, лежащему на шероховатой поверхности, приложить силу , образующую угол α с нормалью (рис.76), то тело сдвинется только тогда, когда сдвигающее усилие Psinα будет больше = f 0 Pcosα. Но неравенство Psinα > f 0 Pcosα, в котором f 0 = , выполняется только при tgα > tg , т.е. при α>ϕ 0 . Следовательно, никакой силой, образующей с нормалью угол α, меньший угла трения , тело вдоль данной поверхности сдвинуть нельзя.

БИЛЕТ – 20

«ТРЕНИЕ КАЧЕНИЯ»

ТРЕНИЕ КАЧЕНИЯ – сопротивление, возникающее при качении одного тела по поверхности другого.

Рассмотрим круглый цилиндрический каток радиуса R и веса Р, лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу (рис.83 а), меньшую . Тогда в точке А возникает сила трения , численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию тоже приложенной в точке А, то она уравновесит силу , а силы и образуют пару, вызывающую качение цилиндра. Фактически следствие деформаций тел касание двух этих цилиндров происходит вдоль некоторой площадки АВ

(рис. 83 б). При действии силы интенсивность давления у края А убывает, а у края В возрастает. В результате реакция оказывается смещенной в сторону действия силы . С увеличением это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара , с моментом Q ПР R и уравновешивающая её пара , с моментом Nk. Из равенства моментов находим Q ПР R = Nk или

Пока QQ ПР начинается качение.

КОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ – входящая в формулу (1) линейная величина k. Измеряют величину k обычно в сантиметрах. Значение коэффициента k зависит от материала тел и определяется опытным путем.

БИЛЕТ – 23

«СПОСОБЫ ОПРЕДЕЛЕНИЯ ЦЕНТРА ТЯЖЕСТИ»

ЦЕНТР ТЯЖЕСТИ – неизменно связанная с данным телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.

1) СИММЕТРИЯ – Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Допустим, например, что однородное тело имеет плоскость симметрии. Тогда этой плоскостью оно разбивается на две такие части, веса которых р 1 и р 2 , равны друг другу, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Следовательно, центр тяжести тела как точка, через которую проходит равнодействующая двух равных и параллельных сил и , будет действительно лежать в плоскости симметрии. Из свойств симметрии следует, что центр тяжести, однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелипипида, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре (центре симметрии) этих тел.

2) РАЗБИЕНИЕ – Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам:

(1)

(2)

При этом, число слагаемых в каждой из сумм будет равно числу частей, на которые разбито тело.

3) ДОПОЛНЕНИЕ – Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

4) ИНТЕГРИРОВАНИЕ – Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объёмы , для которых формулы:

принимают вид:

И Т.Д. , (6)

Где – координаты некоторой точки, лежащей внутри объёма . Затем в равенствах и т.д. переходят к пределу, устремляя все к нулю, т.е. стягивая эти объёмы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространённые на весь объём тела, и формулы (6) дают в пределе:

(7)

Аналогично для координат центров тяжести площадей и линий получаем в пределе из формул (3) и (4):

(8)

(9)

5) ЭКСПЕРИМЕНТАЛЬНЫЙ СПОСОБ – Центры тяжести неоднородных тел сложной конфигурации (самолётов, паровозов и т.д.) можно определять экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.

Между движущимися телами в плоскости их соприкосновения возникает сила трения скольжения . Обусловлено это прежде всего шероховатостью соприкасающихся поверхностей и наличием сцепления у прижатых тел.

В инженерных расчетах обычно пользуются установленными опытным путем закономерностями, которые с некоторой степенью точности отражают действие силы трения. Эти закономерности называют законами трения скольжения (Кулона) . Их можно сформулировать следующим образом.

1. При стремлении сдвинуть одно тело относительно другого в плоскости их соприкосновения возникает сила трения F , модуль которой может принимать любые значения от нуля до Fmax, т. е. . Сила трения приложена к телу и направлена в сторону, противоположную возможному направлению скорости точки приложения силы.

2. Максимальная сила трения равна произведению коэффициента трения f на силу нормального давления N: .

Коэффициент трения f - безразмерная величина, зависящая от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.). Определяют его опытным путем.

Различают коэффициенты трения покоя и трения скольжения, причем последний, как правило, зависит и от скорости скольжения. Коэффициент трения покоя соответствует такой
максимальной силе трения Fmax, при которой имеется предельное состояние равновесия. Малейшее увеличение внешних сил может вызвать движение. Коэффициент трения покоя, как правило, немного больше коэффициента трения скольжения. С увеличением скорости скольжения значение коэффициента трения скольжения сначала незначительно уменьшается, а затем остается практически неизменным. Значения коэффициентов трения для некоторых пар трения следующие: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25; сталь по льду 0,027.

3. Максимальная сила трения в довольно широких пределах не зависит от площади соприкасающихся поверхностей.

Силу трения скольжения иногда называют силой сухого трения .

Реакция шероховатой поверхности. Угол трения .

Реакция идеально гладкой поверхности, как уже говорилось выше, направлена по нормали к поверхности. На шероховатой поверхности могут возникать силы трения скольжения. Поэтому реакцию шероховатой поверхности представим в виде двух составляющих: нормальной реакции N (равна по модулю силе нормального давления) и перпендикулярной ей силы трения F.

Полная реакция R=N + F всегда отклонена от нормали к поверхности на некоторый угол "альфа". На рисунке видно, что . Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу F1, мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения F = -F1, причем . С увеличением силы F1 будет возрастать и сила F . Наконец, при F1 = Fmax наступит предельное состояние равновесия, при котором полная реакция R отклонится от вертикали на угол "альфа"max, называемыйуглом трения . Обозначив его через "фи", получим .

Тангенс угла трения равняется коэффициенту трения. Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения.

Конус трения .

Рассмотрим равновесие невесомого тела на горизонтальной шероховатой плоскости под действием наклонной силы F1, стремящейся его сдвинуть.

Тело будет сдвинуто только тогда, когда > Fmax = . Предельному случаю равновесия соответствует такой угол
наклона a, при котором выполняется равенство = , или tgα = f . Если tgα<=f , то как бы не возрастала сила F1, тело сдвинуть с места невозможно. Возрастающей сдвигающей силе будет противостоять пропорционально ей увеличивающаяся сила трения .