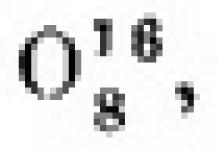Раздел математики который изучает производные функции и их применения, называется дифференциальным исчислением. Это исчисление возникло из решений задач на проведение касательных к кривым, на вычисление скорости движения, на отыскание наибольших и наименьших значений функции.

Ряд задач дифференциального исчисления был решен еще в древности Архимедом, разработавшим способ проведения касательной. Архимед построил касательную к спирали, носящей его имя. Архимед (ок. 287 – 212 до н.э.) – великий ученый. Первооткрыватель многих фактов и методов математики и механики, блестящий инженер.

Задача нахождения скорости изменения функции была впервые решена Ньютоном. Задача нахождения скорости изменения функции была впервые решена Ньютоном. Функцию он назвал флюэнтой, т.е. текущей величиной. Производную – ф л ю к с и е й. Функцию он назвал флюэнтой, т.е. текущей величиной. Производную – ф л ю к с и е й. Ньютон пришел к понятию производной исходя из вопросов механики. Исаак Ньютон (1643 – 1722 гг.) – английский физик и математик.

Основываясь на результатах Ферма и некоторых других выводах, Лейбниц в 1684 году опубликовал первую статью по дифференциальному исчислению, в которой были изложены основные правила дифференцирования. Лейбниц Готфрид Фридрих (1646 – 1716) – великий немецкий ученый, философ, математик, физик, юрист, языковед

Применение производной: Применение производной: 1) Мощность – это производная работы по времени P = A" (t). 2) Сила тока – производная от заряда по времени I = g" (t). 3) Сила – есть производная работы по перемещению F = A" (x). 4) Теплоемкость – это производная количества теплоты по температуре C = Q" (t). 5) Давление – производная силы по площади P = F"(S) 6) Длина окружности – это производная площади круга по радиусу l окр =S" кр (R). 7) Темп роста производительности труда – это производная производительности труда по времени. 8) Успехи в учебе? Производная роста знаний.

Применение производной в физике Задача: Два тела движутся прямолинейно соответственно по законам: S 1 (t) = 3,5t 2 – 5t + 10 и S 2 (t) = 1,5t 2 +3t –6. В какой момент времени скорости тел будут равны? Задача: Два тела движутся прямолинейно соответственно по законам: S 1 (t) = 3,5t 2 – 5t + 10 и S 2 (t) = 1,5t 2 +3t –6. В какой момент времени скорости тел будут равны?

Применение производной в экономике Задача: Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накоплений предприятия от объема выпуска выражается формулой Задача: Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накоплений предприятия от объема выпуска выражается формулой Исследовать потенциал предприятия. Исследовать потенциал предприятия. 15

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ

Выполнила: Вербицкая Елена Вячеславовна

преподаватель математики ГАПОУ СО

«Энгельсский политехникум»

Введение

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, чтопроизводная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y =f (x ) в точке x 0 – это скорость изменения функции f (x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y " , f " ввёл Ж.Лагранж в 1797г.

Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о, - это прямая, проходящая через точку (x о; f (x о)) и имеющая угловой коэффициент f ′(x о).

y = f (x о) + f ′(x о) (x – x о)

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

выпуклым , если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов = - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)

Производная в биологии:

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Производная в географии:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

у’= к у

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010

8. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

Периодические источники:

Газеты и журналы: «Математика», «Открытый урок»

Использование ресурсов сети Интернет, электронных библиотек.

Производная функции в точке является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различного рода процессов.

Основные определения

Производная равна пределу отношения приращения функции к приращению аргумента , при условии, что последний стремится к нулю:

$y^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}$

Определение

Функция, которая имеет конечную производную в некоторой точке, называется дифференцируемой в данной точке . Процесс вычисления производной называется дифференцированием функции .

Историческая справка

Русский термин "производная функции" впервые употребил русский математик В.И. Висковатов (1780 - 1812).

Обозначение приращения (аргумента/функции) греческой буквой $\Delta$ (дельта) впервые употребил швейцарский математик и механик Иоганн Бернулли (1667 - 1748). Обозначение дифференциала , производной $d x$ принадлежит немецкому математику Г.В. Лейбницу (1646 - 1716). Манера обозначать производную по времени точкой над буквой - $\dot{x}$ - идёт от английского математика, механика и физика Исаака Ньютона (1642 - 1727). Краткое обозначение производной штрихом - $f^{\prime}(x)$ - принадлежит французскому математику, астроному и механику Ж.Л. Лагранжу (1736 - 1813), которое он ввел в 1797 году. Символ частной производной $\frac{\partial}{\partial x}$ активно применял в своих работах немецкий математик Карл Г.Я. Якоби (1805 - 1051), а затем выдающийся немецкий математик Карл Т.В. Вейерштрасс (1815 - 1897), хотя это обозначение уже встречалось ранее в одной из работ французского математика А.М. Лежандра (1752 - 1833). Символ дифференциального оператора $\nabla$ придумал выдающийся ирландский математик, механик и физик У.Р. Гамильтон (1805 - 1865) в 1853 году, а название "набла" предложил английский ученый-самоучка, инженер, математик и физик Оливер Хевисайд (1850 - 1925) в 1892 году.

История появления понятия производной

Функции, границы, производная и интеграл являются базовыми понятиями математического анализа, изучаемыми в курсе средней школы. И понятие производной неразрывно связано с понятием функции.

Термин "функция" впервые был предложен немецким философом и математиком для характеристики разных отрезков, соединяющих точки некоторой кривой в 1692 г. Первое определение функции, которое уже не было связано с геометрическими представлениями, сформулировал в 1718г. Ученик Иоганна Бернулли

в 1748. уточнил определение функции . Заслугам Эйлера приписывают введение для обозначения функции символ f (х).

Строгое определение предела и непрерывности функции сформулировал в 1823 г. Французский математик Огюстен Луи Коши . Определение непрерывности функции еще раньше Коши сформулировал чешский математик Бернард Больцано . По этим определениям на базе теории действительных чисел было осуществлено строгое обоснование основных положений математического анализа.

Открытию подходов и основ дифференциального исчисления предшествовали работы французского математика и юриста , который в 1629 г. предложил способы нахождения наибольших и наименьших значений функций, проведение касательных к произвольным кривым, фактически опирались на применение производных. Этому способствовали также работы , разработавший метод координат и основы аналитической геометрии. Лишь в 1666 году и несколько позднее независимо друг от друга построили теорию дифференциального исчисления. Ньютон пришел к понятию производной, решая задачи о мгновенной скорости, а , - рассматривая геометрическую задачу о проведении касательной к кривой. и исследовали проблему максимумов и минимумов функций.

Интегральное исчисление и само понятие интеграла возникли из потребностей вычисления площадей плоских фигур и объемов произвольных тел. Идеи интегрального исчисления берут начало в работах древних математиков. Однако это свидетельствует "метод исчерпывания" Евдокса, который позже использовал в III в. до н. э Суть этого метода заключалась в том, что для вычисления площади плоской фигуры и, увеличивая число сторон многоугольника, находили границу, в которую направлялись площади ступенчатых фигур. Однако для каждой фигуры вычисления предела зависело от выбора специального приема. А проблема общего метода вычисления площадей и объемов фигур оставалась нерешенной. Архимед еще явно не применял общее понятие границы и интеграла, хотя в неявном виде эти понятия использовались.

В XVII в. , открывший законы движения планет, была успешно осуществлена первая попытка развить идеи . Кеплер вычислял площади плоских фигур и объемы тел, опираясь на идею разложения фигуры и тела на бесконечное количество бесконечно малых частей. Из этих частей в результате добавления состояла фигура, площадь которой известно и позволяющая вычислить площадь искомой. В историю математики вошел так называемый "принцип Кавальери", с помощью которого вычисляли площади и объемы. Этот принцип получил теоретическое обоснование позже с помощью интегрального исчисления.
Идеи и других ученых стали той почвой, на котором Ньютон и Лейбниц открыли интегральное исчисление. Развитие интегрального исчисления продолжили и гораздо позже Пафнутий Львович Чебышев разработал способы интегрирования некоторых классов иррациональных функции.

Современное определение интеграла как предела интегральных сумм принадлежит Коши . Символ

Https://ppt4web.ru/images/1345/36341/310/img0.jpg" alt="Презентация на тему:Производная. Выполнили ученицы 11»а»класса:Челобитчикова Мар" title="Презентация на тему:Производная. Выполнили ученицы 11»а»класса:Челобитчикова Мар">

Описание слайда:

№ слайда 2

Описание слайда:

№ слайда 3

Описание слайда:

Из истории: В истории математики традиционно выделяются несколько этапов развития математических знаний:Формирование понятия геометрической фигуры и числа как идеализации реальных объектов и множеств однородных объектов. Появление счёта и измерения, которые позволили сравнивать различные числа, длины, площади и объёмы. Изобретение арифметических операций. Накопление эмпирическим путём (методом проб и ошибок) знаний о свойствах арифметических действий, о способах измерения площадей и объёмов простых фигур и тел. В этом направлении далеко продвинулись шумеро-вавилонские, китайские и индийские математики древности. Появление в древней Греции дедуктивной математической системы, показавшей, как получать новые математические истины на основе уже имеющихся. Венцом достижений древнегреческой математики стали «Начала» Евклида, игравшие роль стандарта математической строгости в течение двух тысячелетий. Математики стран ислама не только сохранили античные достижения, но и смогли осуществить их синтез с открытиями индийских математиков, которые в теории чисел продвинулись дальше греков. В XVI-XVIII веках возрождается и уходит далеко вперёд европейская математика. Её концептуальной основой в этот период являлась уверенность в том, что математические модели являются своего рода идеальным скелетом Вселенной, и поэтому открытие математических истин является одновременно открытием новых свойств реального мира. Главным успехом на этом пути стала разработка математических моделей зависимости (функция) и ускоренного движения (анализ бесконечно малых). Все естественные науки были перестроены на базе новооткрытых математических моделей, и это привело к колоссальному их прогрессу. В XIX-XX веках становится понятно, что взаимоотношение математики и реальности далеко не столь просто, как ранее казалось. Не существует общепризнанного ответа на своего рода «основной вопрос философии математики»: найти причину «непостижимой эффективности математики в естественных науках». В этом, и не только в этом, отношении математики разделились на множество дискутирующих школ. Наметилось несколько опасных тенденций: чрезмерно узкая специализация, изоляция от практических задач и др. В то же время мощь математики и её престиж, поддержанный эффективностью применения, высоки как никогда прежде

№ слайда 4

Описание слайда:

№ слайда 5

Описание слайда:

Дифференцируемость Производная f"(x0) функции f в точке x0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x0 тогда и только тогда, когда её производная в этой точке существует и конечна: Для дифференцируемой в x0 функции f в окрестности U(x0) справедливо представлениеf(x) = f(x0) + f"(x0)(x − x0) + o(x − x0)

№ слайда 6

Описание слайда:

Замечания Назовём Δx = x − x0 приращением аргумента функции, а Δy = f(x0 + Δx) − f(x0) приращением значения функции в точке x0. Тогда Пусть функция имеет конечную производную в каждой точке Тогда определена производная функция Функция, имеющая конечную производную в точке, непрерывна в ней. Обратное не всегда верно. Если производная функция сама является непрерывной, то функцию f называют непрерывно дифференцируемой и пишут:

№ слайда 7

Описание слайда:

Геометрический и физический смысл производной Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x - x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 - C1). Тангенс угла α наклона этой касательной - и есть производная в точке x0.

№ слайда 8

Описание слайда:

Производные высших порядков Понятие производной произвольного порядка задаётся рекуррентно. Полагаем Если функция f дифференцируема в x0, то производная первого порядка определяется соотношением Пусть теперь производная n-го порядка f(n) определена в некоторой окрестности точки x0 и дифференцируема. Тогда

№ слайда 9

Описание слайда:

Способы записи производных В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:Лагранжа f(n)(x0), при этом для малых n часто используют штрихи и римские цифры: f(1)(x0) = f"(x0) = fI(x0),f(2)(x0) = f""(x0) = fII(x0),f(3)(x0) = f"""(x0) = fIII(x0),f(4)(x0) = fIV(x0), и т. д.Такая запись удобна своей краткостью и широко распространена;Лейбница, удобная наглядной записью отношения бесконечно малых: Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например: - производная первого порядка x по t при t = t0, или - вторая производная f по x в точке x0 и т.д.Эйлера, использующая дифференциальный оператор (строго говоря, дифференциальное выражение, пока не введено соответствующее функциональное пространство), и потому удобная в вопросах, связанных с функциональным анализом: , Конечно, при этом надо не забывать, что служат все они для обозначения одних и те же объектов:

№ слайда 10

Описание слайда:

Примеры: Пусть f(x) = x2. Тогда Пусть f(x) = | x | . Тогда если то f"(x0) = sgnx0,где sgn обозначает функцию знака. Если x0 = 0, то а следовательно f"(x0) не существует

№ слайда 11

Описание слайда:

Правила дифференцирования Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. (производная суммы равна сумме производных) (отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу) Если функция задана параметрически: то,